周波数応答解析(モード法)|Abaqusチュートリアル
(Abaqusバージョン:Abaqus 6.9 Student Edition)
周波数応答解析に関する詳しい説明は『動解析入門』を参照してください。ここではAbaqusによるモデル化方法に関して説明します。ちなみにAbaqusでは周波数応答解析を定常調和動的応答解析と呼ぶようです。
 |
-
<目次>
- 概要
- 解析ステップの定義
- 荷重条件の定義
- 解析ジョブの作成と投入
- 解析結果の表示
概要
本項では前項で作成したプレートの固有値解析モデルの先端に正弦波荷重を追加し、モーダル法で周波数応答解析を実施する方法について説明します。本項でのモデリングを始める前に、予め前項のモデルを開いて別名保存をしておいてください。
解析条件
- プレート寸法:300×50×1.2
- 材料:鉄鋼材料を想定(E=210GPa,ρ=7.85e-6kg/mm^3,ν=0.3)
- 拘束条件:片側の端部を完全固定
- 荷重条件:梁の先端に1Nの正弦波荷重(周波数範囲:1〜100Hz)
- 固有値抽出範囲:1〜500Hz
- 減衰:1〜500Hzの範囲で減衰比0.05
モデルの外観は以下です。

(→このページのトップに移動)
解析ステップの定義
解析ステップの作成方法
モデルツリーにおいて、ステップの右クリックメニューから"作成"を選択します。この時、ステップモジュールに自動で切り替わります。

上記操作で現れる"ステップの作成"ダイアログにおいて、このステップの後に新しいステップを追加で、Step-1(固有値解析のステップ)を選択、名前にStep-2(デフォルト)、プロシージャタイプ:線形摂動、Steady-state dynamics,Modal を選択して、続けるボタンをクリックします。

今回はモード法で周波数応答解析を実施します。直接法で解析する場合にはSteady-state dynamics,Directを選択します。
上記操作で現れる"ステップの編集"ダイアログの基本タブにおいて、スケール:線形、振動数の下限値:1、振動数の上限値:100Hz、応答計算点の数:496、バイアス:1と入力します。これは周波数刻み幅(Δf)=0.2Hzで計算する設定となります。ちなみに応答点の数は(振動数の上限値-下限値)÷Δf+1となります。
(参考)
周波数応答解析におけるΔfを見積もる方法
モード法の周波数応答、過渡応答解析におけるモード数

次に減衰タブにおいて、次の範囲で減衰を指定:振動数、直接減衰データを使用するにチェック、振動数と臨界減衰比の関係で1〜500Hzで0.05と入力します。

周波数によってモード減衰比を変化させたいときは行を増やして適切に設定します。今回は一律で0.05としました。
設定が完了しましたらOKボタンをクリックしてダイアログを閉じます。
フィールド出力要求の設定
周波数応答解析のフィールド出力を設定します。上記で周波数応答解析のステップを定義すると、自動で新たなフィールド出力F-Output-2が設定されます。このF-Output-2の右クリックメニューから"編集"をクリックします。

今回はデフォルトの設定を受け入れます。フィールド出力要求の編集ダイアログの設定項目を確認にしてOKボタンをクリックします。

<補足>
今回のモデルは要素数が少ないのであまり問題になりませんが、大規模モデルになると、すべての節点、要素の解析結果を出力すると膨大なファイルサイズなることも考えられます。その場合、領域をモデル全体ではなく、集合などで評価したい節点などを指定し、履歴出力要求するとよいでしょう。
(→このページのトップに移動)
荷重条件の設定
モデルツリーにおいて、荷重の項目の右クリックメニューから"作成"を選択します。この時、荷重モジュールに自動で切り替わります。

上記操作で現れる"荷重の作成"ダイアログにおいて、ステップで周波数応答解析のStep-2を選択、カテゴリで機械的、タイプでシェルエッジ力を選択し、続けるのボタンをクリックします。名前を適宜変更しても構いません。

次にビューポート上で荷重を設定するエッジを選択します。拘束部とは反対側の端部のエッジを選択し(下図では上端のエッジを選択)、完了ボタンをクリック。

上記操作で現れる"荷重の編集"ダイアログにおいて、分布:均一、力:一般、方向は編集ボタンにて:最初のポイント(0,0,0)、2番目のポイント(0,0,1)、大きさ:(実部に)1000/50、と入力します。荷重の大きさは1[N]をmN(ミリニュートン)単位で入力しています。さらに、シェルエッジ力は単位長さ当たりの荷重であるのでエッジ長さ(50mm)で割っています。また、これは線形解析には関係ありませんが、力は次の単位領域で定義:原形領域、一番下の"回転に従う"のチェックを外します。

参考:振動の複素数表現について
(→このページのトップに移動)
解析ジョブの作成と投入
解析ジョブの作成
解析モデルが完成したので、解析ジョブを作成して計算を実行してみましょう。モデルツリーにおいて解析を展開してジョブの項が表示されるようにします。今回は前回実施した固有値解析のモデルをベースにしているので、その時のジョブが残っています。ジョブ名の右クリックメニューから"名前の変更"を選択します。

上記操作で現れる"ジョブの作成"ダイアログでジョブの名前にplate_ssd_modal_jobと入力し、"OK"ボタンをクリックします。変更するジョブ名は任意です。

ワーキングディレクトリの設定
解析結果のファイルやログファイルなどはワーキングディレクトリに作成されます。予め設定しておかないと、どこにファイルが保存されたのか解らなくなってしまうこともありますので、一応設定しておきましょう。
ファイルメニューからワーキングディレクトリの設定を選択します。ご自身の環境に合わせて設定ください。モデルファイルと同じディレクトリの方が解りやすいかもしれません。
解析ジョブの投入
モデルツリーにおいて、先ほど定義したジョブplate_ssd_modal_jobの右クリックメニューから"ジョブの投入"を選択します。この操作で計算が実行されます。計算が実行中はジョブ名の横に"実行中"と表示され、計算が終了すると"完了"に変わります。

plate_ssd_modal_jobの右クリックメニューから"モニタ"を選択しますと、解析の進行状況を確認することができます。ログの窓に完了と表示されれば計算終了です。

(→このページのトップに移動)
解析結果の表示
結果ファイルの読み込み
モデルツリーにおいて、ジョブ名(plate_ssd_modal_job)の右クリックメニューから"結果"をクリックします。

応答のグラフ作成
今回は振動の応答をグラフで表示する方法について説明します。メニューからツール/XYデータ/マネージャを選択します。

XYデータマネージャにおいて、作成ボタンをクリックします。

XYデータの作成ダイアログにおいて、ODBフィールド出力をクリックします。

ODBフィールド出力からのXYデータダイアログにおいて、位置:節点、編集フィールドで空間加速度/Magnitudeを選択します。ここでは加速度の絶対値としましたが、評価したい項目をここで自由に選択することができます。

上記ダイアログで”有効なステップ/フレーム”のボタンをクリックします。
有効なステップ/フレームダイアログにおいて、周波数応答解析のステップのみが選択されるように、Step-1のチェックを外します。緑のチェックがStep-2のみに付くようにしたら、OKボタンをクリックします。

ODBフィールド出力からのXYデータダイアログにおいて、要素/節点タブをクリックしてタブを切り替えます。"選択の編集"ボタンをクリックして、ビューポート上で評価したい節点をクリックします。

ここでは下図のようにプレートの先端エッジの中心を選択しました。赤い点が選択した節点です。選択できましたらプロンプトエリアの"完了"ボタンをクリックします。

ODBフィールド出力からのXYデータダイアログにおいて、"プロット"ボタンをクリックします。

そうしますと、ビューポートに下図のような応答波形が表示されます。しかしなんだか変なグラフですね。なぜか固有振動数の11.3Hz、70.6Hz付近で応答レベルが下がっています。周波数応答解析に限らず振動解析における応答波形は一般に複素数となりますが、どうやらAbaqusではデフォルトで実部のみを表示する設定となっているためにこのようなグラフになるようです。

ということで振幅の大きさを正しく表示できるように設定します。
メニューから結果/オプションを選択します。

結果オプションダイアログにおいて、”複素数の形式”タブを選択、数値形式で”大きさ”にチェックを入れます。よければ"OKボタン"をクリックします。

この設定の後、もう一度グラフを作成してみてください。今度は以下のようになるはずです。
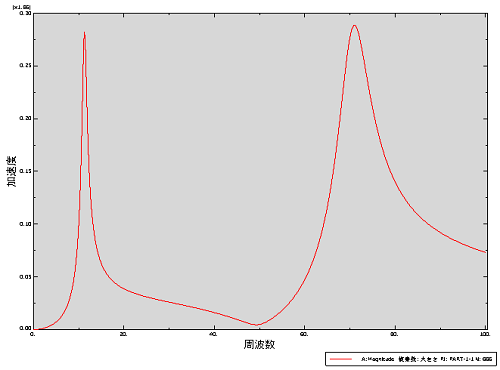
今回は加速度について表示させてみましたが、速度や変位についても同様の操作ですのでやってみてください。
グラフデータの抽出
グラフのデータは以下の操作で編集することができます。
グラフが表示された状態で、再度XYデータマネージャを開きます(メニューバーから、ツール/XYデータ/マネージャ)。
XYデータマネージャダイアログで表示されているグラフのデータを選択して編集ボタンをクリックします。

XYデータの編集ダイアログにより、描画データを直接編集することができます(ねつ造はいけませんよ)。私はこのデータをコピーしてエクセルで活用するのに使っています。

(→このページのトップに移動)
