7.怳摦摿惈傪峫椂偟偨峔憿愝寁偺峫偊曽乥婡夿椡妛
幚嵺偺峔憿暔偵偍偗傞怳摦尰徾偼丄偙傟傑偱愢柧偟偰偒偨1帺桼搙偺怳摦偺傛偆偵扨弮偱偼偁傝傑偣傫丅偟偐偟丄暋嶨側尰徾傪1帺桼搙偺尰徾偵抲偒姺偊偰峫偊傞偙偲偱丄栤戣偺杮幙偑棟夝偟堈偔側傝丄専摙拞偺峔憿暔偵怳摦揑側栤戣偑偁偭偨偲偟偰傕揔愗側懳墳偑庢傟傞傛偆偵側傝傑偡丅杮崁偱偼娙扨側帠椺傪尦偵怳摦摿惈傪峫椂偟偨峔憿愝寁偺峫偊曽偵偮偄偰愢柧偟傑偡丅
怳摦尰徾偺尨棟丒尨懃
偙傟傑偱愢柧偟偰偒偨撪梕偼彮乆悢妛揑側偺偱丄偙傟傪媄弍幰偵偲偭偰棟夝偟堈偄尵偄曽偵曄偊偰傑偲傔偰傒傑偡丅
怳摦栤戣偵娭楢偟偨峔憿専摙偺撪梕偵偼戝偒偔暘偗偰2庬椶偁傞偲峫偊傜傟傑偡丅1偮偼怳摦傪敪惗偡傞憰抲傪偽偹偱巟帩偡傞峔憿偵娭偡傞傕偺丅偙傟偼庡偵怳摦愨墢傪庡側栚揑偲偟偰偍傝丄慜崁偱愢柧偟偨怳摦揱払棪偺峫偊曽偑偦偺傑傑揔梡偱偒傑偡丅嬶懱椺傪嫇偘傞偲丄僄儞僕儞偲僄儞僕儞儅僂儞僩偺娭學傪僀儊乕僕偡傞偲傢偐傝傗偡偄偲巚偄傑偡丅傕偆堦偮偼怳摦傪敪惗偡傞憰抲傪巟偊偰偄傞懁偺怳摦摿惈偵娭偡傞傕偺丅偙傟偼庴偗偨怳摦偺椡偦偺傕偺偼嫋梕偟傑偡偑丄偦傟傪擛壗偵憹暆偝偣側偄傛偆偵偡傞偐偑尞偵側傝傑偡丅嬶懱椺傪嫇偘傞偲丄僄儞僕儞傪搵嵹偟偨僼儗乕儉懁偺怳摦摿惈偵憡摉偟傑偡丅偦傟偧傟偵偮偄偰専摙偡傞応崌偺億僀儞僩偵偮偄偰傑偲傔傑偡丅
嘆怳摦傪敪惗偡傞憰抲傪偽偹偱巟帩偡傞峔憿傪専摙偡傞応崌偺億僀儞僩
- 偽偹偱巟帩偝傟偨憰抲偺屌桳怳摦悢偼丄怳摦尮偺廃攇悢偵懳偟偰彮側偔偲傕1/併2埲壓丄廫暘側怳摦愨墢岠壥傪摼傞偵偼1/3埲壓偵側傞傛偆偵偡傞丅偨偩偟丄尭悐傪戝偒偔偡傞偲怳摦愨墢岠壥偑埆偔側傞嫲傟偑偁傞(仸)丅
- 屌桳怳摦悢傪掅偔偡傞偵偼丄偽偹掕悢傪彫偝偔偡傞曽朄(K傪彫偝偔偡傞)丄憰抲帺懱傪廳偔偡傞(m傪戝偒偔偡傞)偑偁傞丅
- 怳摦尮偺壱摦廃攇悢斖埻偵偳偆偟偰傕偦偺憰抲偺屌桳怳摦悢偑擖偭偰偒偰偟傑偆応崌偼丄廫暘側尭悐傪梌偊傞偙偲偱丄嫟怳帪偺怳摦傪梷偊傞偙偲偑偱偒傞丅
仸)懍搙埶懚偺尭悐偺応崌偺榖丅僑儉偺傛偆側僸僗僥儕僔僗尭悐傪桳偡傞嵽椏傪偽偹偲偟偰梡偄傞応崌丄兝>併2偱偺揱払棪偼尭悐偑側偄応崌偲傎偲傫偳曄傢傜側偄丅
偙偺応崌偼僄儞僕儞儅僂儞僩傪僀儊乕僕偡傞偲夝傝堈偄偲巚偄傑偡丅傾僀僪儕儞僌忬懺偺帪偺廃攇悢偼偦偺宯偺屌桳怳摦悢偺彮側偔偲傕併2攞丄廫暘側怳摦愨墢岠壥傪摼傞偵偼3攞埲忋棧傟偰偄傞昁梫偑偁傝傑偡丅傑偨丄僄儞僕儞巒摦帪偼偳偆偟偰傕偦偺宯偺屌桳怳摦悢傪捠傝傑偡偺偱丄堦弖偱偡偑嫟怳偼旔偗傜傟傑偣傫丅偦偺帪偺怳暆傪梷偊傞偵偼尭悐傪壛偊傞偟偐偁傝傑偣傫丅
嘇怳摦傪敪惗偡傞憰抲傪巟偊偰偄傞懁偺怳摦摿惈傪専摙偡傞応崌偺億僀儞僩
- 怳摦傪敪惗偡傞憰抲傪巟偊偰偄傞懁偺峔憿(埲屻婎慴偲屇傇)偺屌桳怳摦悢偼丄婎杮揑偵憰抲偺壱摦怳摦悢偺斖埻偵擖傜側偄傛偆偵婎慴懁偺摦揑側崉惈傪専摙偡傞丅堦斒偵偼婎慴懁偺怳摦悢偑憰抲偺壱摦怳摦悢傛傝崅偔側傞傛偆偵偡傞丅(偦偺媡偺応崌丄婎慴偺崉惈偑掅偔側傝偡偓偰丄梫媮偝傟傞偟偭偐傝巟偊傞婡擻傪枮懌偟側偔側傞壜擻惈偑偁傞偨傔)
- 婎慴偺屌桳怳摦悢傪崅偔偡傞偵偼丄峔憿偺崉惈傪忋偘傞曽朄(K傪戝偒偔偡傞)丄寉偔偡傞曽朄(m傪彫偝偔偡傞)偑偁傞丅
- 傗傓傪摼偢丄憰抲偺壱摦怳摦悢斖埻偵婎慴偺屌桳怳摦悢偑擖偭偰偒偰偟傑偆応崌偼丄廫暘側尭悐傪梌偊傞偙偲偱丄嫟怳帪偺怳摦傪梷偊傞偙偲偑偱偒傞丅
偙偺応崌丄僄儞僕儞傪僄儞僕儞儅僂儞僩傪夘偟偰巟偊傞僼儗乕儉傪僀儊乕僕偡傞偲夝傝堈偄偲巚偄傑偡丅僼儗乕儉偑庛偔偰偼榖偵側傝傑偣傫丅偱偒傞偩偗崉惈傪忋偘傞偙偲偱僄儞僕儞偺廃攇悢斖埻偵僼儗乕儉懁偺屌桳怳摦悢偑擖傜側偄傛偆偵専摙偟傑偡丅偲偼偄偊偙傟偑側偐側偐擄偟偔丄摿偵壒偺椞堟傑偱偲側傞偲丄僷僱儖偺嫟怳側偳旔偗傜傟側偄偔側傞応崌傕偁傝傑偡丅偦偺応崌偼尭悐岠壥傪忋偘傞偨傔偵丄惂怳嵽側偳傪妶梡偟偰嫟怳帪偺怳暆傪梷偊傞懳嶔傕巤偝傟傑偡丅
幚嵺偺峔憿偵偍偄偰丄怳摦偺儌乕僪(宍懺)偼暋悢懚嵼偟傑偡偑丄暋嶨側怳摦尰徾偱傕丄撍偒媗傔傟偽屄乆偺怳摦儌乕僪偺廳偹崌傢偣偲偟偰昞尰偝傟傑偡丅偟偨偑偭偰丄偦傟偧傟偺怳摦偺儌乕僪偼撈棫偵峫偊傞偙偲偑偱偒丄偙傟傑偱愢柧偟偰偒偨傛偆側1帺桼搙偺怳摦偺峫偊曽偑偦偺傑傑揔梡偱偒傞偺偱偡丅
夝愅椺
嘆偺応崌偵偮偄偰丄6帺桼搙崉懱怳摦僔儈儏儗乕僔儑儞僜僼僩僂僃傾丄PTMT偺儅僯儏傾儖偱徯夘偟偰偄傞僒儞僾儖傪椺偵偟偰愢柧偟傑偡丅
夝愅儌僨儖
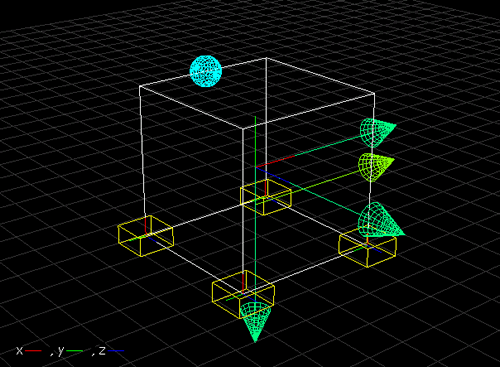
傑偢夝愅儌僨儖丄壓恾偼扨弮側棫曽懱偺幙検梫慺傪4偮偺偽偹偱巟帩偟偨儌僨儖偱偡丅偙傟傪僄儞僕儞偲憐掕偟偰偔偩偝偄丅偦偟偰偙偺儌僨儖忋偺墿椢怓偺栴報偑僄儞僕儞偺僋儔儞僋幉偵壛傢傞僩儖僋曄摦偺椡偲憐掕偟傑偡丅偦偺懠偄傠偄傠栴報偑偁傝傑偡偑丄偙偙偱偼偲傝偁偊偢柍帇偟偰偔偩偝偄丅墿怓偺棫曽懱偑4偮偁傝傑偡偑丄偙傟偑儅僂儞僩偵側傝傑偡丅
偙偙偱偼傾僀僪儕儞僌偺廃攇悢偲偟偰25Hz傪憐掕偟傑偡丅偟偨偑偭偰偙偺廃攇悢偱偺僄儞僕儞偺怳摦儗儀儖偑栤戣偲側傝傑偡丅
夝愅寢壥
偙偺儌僨儖偺僩儖僋曄摦偵傛傞僄儞僕儞偺怳摦傪夝愅偟偨寢壥偑埲壓偱偡丅廲幉偼僋儔儞僋幉偵増偭偨嵗昗幉(x幉)廃傝偺夞揮妏傪昞偟偰偄傑偡丅墶幉偼廃攇悢偱1Hz偐傜50Hz傑偱寁嶼偟偰偄傑偡丅
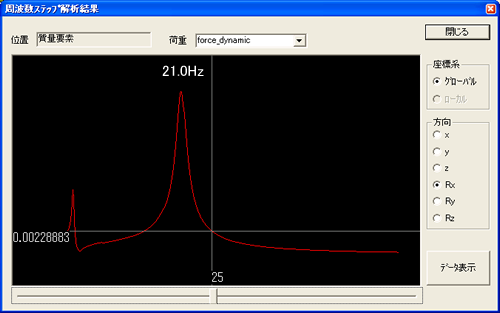
嶳偑2偮偁傝傑偡偑偙傟偼x幉廃傝偺夞揮(Rx)惉暘傪娷傫偩儌乕僪(埲屻儘乕儕儞僌儌乕僪偲屇傃傑偡)偱偁傝丄6.5Hz偲21Hz偵偁傝傑偡丅
偙偺夝愅儌僨儖偱偼傾僀僪儕儞僌廃攇悢25Hz偑儘乕儕儞僌偺屌桳怳摦悢21Hz偵懳偟偰併2攞埲忋棧傟偰偄傑偣傫偺偱丄怳摦揱払棪偑1埲忋偵側傝丄怳摦愨墢偺岠壥偑側偔丄傓偟傠僼儗乕儉懁偵憹暆偝傟偨椡傪揱払偟偰偟傑偭偰偄傞偙偲偵側傝傑偡丅偍偦傜偔偙偺忬懺偱幵椉偵搵嵹偡傞偲僆儁儗乕僞偑姶偠傞怳摦偼偐側傝埆偔側傞偺偱偼側偄偱偟傚偆偐丅幚嵺偵偼幵懱偺崉惈偦偺懠傕塭嬁偟傑偡偺偱丄堦奣偵偼尵偊傑偣傫偑丄怳摦愨墢傪栚揑偲偟偰儅僂儞僩傪夘偟偰偄傞偺偱偡偐傜丄偙偺傛偆側愝寁偼偡傋偒偱偼偁傝傑偣傫丅
懳嶔専摙
偱偼懳嶔傪峫偊偨偄偲巚偄傑偡丅堦斣娙扨側偺偼偽偹掕悢傪彫偝偄抣偵愝掕偟偰廮傜偐偔偡傞偙偲偱偡丅偟偐偟偦傟偱偼偪傚偭偲寍偑側偄偱偡偟丄巟帩崉惈偺柺偱栤戣偑弌偰偒傑偡偺偱丄偙偙偱偼儅僂儞僩偺埑弅曽岦偺偽偹掕悢偲偣傫抐曽岦偺偽偹掕悢偺堘偄傪棙梡偡傞偙偲偱丄偽偹掕悢傪曄偊偢偵儘乕儕儞僌怳摦悢傪掅偔偡傞偙偲傪峫偊傑偡丅堦斒偵儅僂儞僩偲偟偰僑儉傪梡偄傞応崌丄埑弅曽岦偵懳偟偰偣傫抐曽岦偺偽偹掕悢偑彫偝偔側傝傑偡丅宍忬偵傕傛傝傑偡偑巐妏偄僽儘僢僋忬偺宍忬偺応崌丄1/5掱搙偵偼側傝傑偡丅偟偨偑偭偰丄儘乕儕儞僌曽岦偺曄埵偵懳偟偰丄儅僂儞僩偑偣傫抐曽岦偱偦偺椡傪庴偗傞傛偆偵儅僂儞僩偵孹幬傪偮偗偰攝抲偡傟偽傛偄偙偲偵側傝傑偡丅
壓恾偱偼偲傝偁偊偢30亱偺孹幬傪偮偗偰攝抲偟偰傒傑偟偨丅
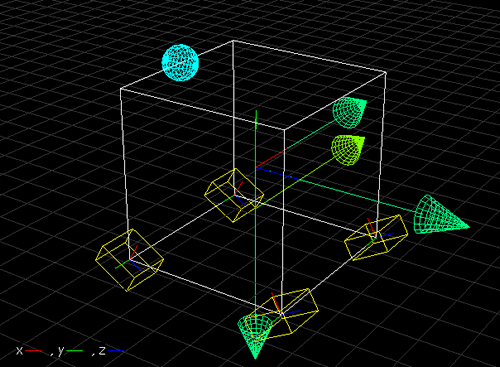
偙偺儌僨儖偵偍偄偰夝愅偟偨寢壥偑埲壓偱偡丅廲幉偵僄儞僕儞偺儘乕儕儞僌曽岦偺夞揮妏傪丄墶幉廃攇悢傪偲偭偰僾儘僢僩偟偰偄傑偡丅
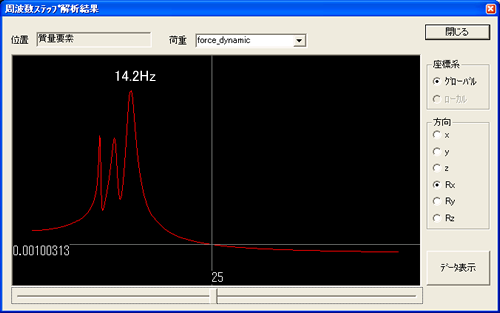
嵟戝偺儘乕儕儞僌廃攇悢偼14.2Hz偲側傝傑偟偨丅偲傝偁偊偢併2攞埲忋棧偡偙偲偼偱偒傑偟偨丅傾僀僪儕儞僌廃攇悢25Hz帪偺僄儞僕儞怳摦偵偮偄偰傕丄曄埵妏偱1/2埲壓(0.0023仺0.0010)偵偡傞偙偲偑偱偒傑偟偨丅偲偄偆偙偲偼怳摦壛懍搙傕1/2埲壓偵側偭偨偲偄偆偙偲偵側傝傑偡丅
幚嵺偵偼怳摦揑側摿惈偺懠偵巟帩崉惈傗儅僂儞僩偺傂偢傒(懴媣惈)側偳丄偦偺懠偨偔偝傫偺崁栚偵偮偄偰徻嵶偵専摙偟偰丄攝抲傗偽偹掕悢傪寛掕偟傑偡丅偁偔傑偱僒儞僾儖偱偡偺偱丄娙扨偵堦椺傪徯夘偟傑偟偨丅
