6.振動伝達率｜機械力学

これまで、非減衰あるいは減衰系の強制振動モデルの特性を評価するのに、振幅倍率を用いてきましたが、ここでさらに重要な概念である振動伝達率について考えてみたいと思います。

振動伝達率の概念

振動伝達率は支持点の反力の大きさと、振動源から入力される力の比で定義されます。つまり、ばねによって支持点に伝える振動の力をどのくらい低減できているかを表すパラメータということができます。振動を絶縁するためには、できるだけ振動伝達率を小さく抑えることが重要になります。

振動伝達率について考察することにより、振動問題に対するアプローチ法が自ずと見えてきます。導出方法も含めてぜひとも理解していただきたい。

繰り返しになりますが、振動伝達率は支持点の反力の大きさと、振動源から入力される力の比で定義されます。入力される力の大きさは式(5-1)の右辺のようにFで定義されていますので、支持点の反力をどのように導くかがポイントです。

まず、前項で導いた減衰強制振動の解を改めて下式に示します。

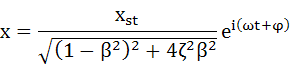・・・(6-1)

ここで、計算を簡単にするために変位振幅の大きさの部分を式(6-2)のように定義します。

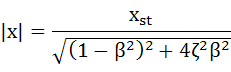・・・(6-2)

すると式(6-1)は式(6-3)のようになります。ここでφは位相で前項にも出てきていますが、改めて式(6-4)として記します。

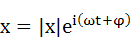・・・(6-3)

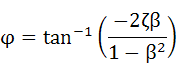・・・(6-4)

さて、ここからとりあえず支持点の反力を求めていきます。
支持点の反力(ここではFtと表記)は、ばねの変位により発生する力(ここではFsと表記)と変位速度によって発生する減衰力(ここではFdと表記)の和として表すことができます。

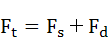・・・(6-5)

Ft：支持点の反力、Fs：ばねの変位により発生する力、Fd：変位速度によって発生する減衰力

それぞれの力は減衰強制振動の解である式(6-3)を用いて、以下のように表すことができます。

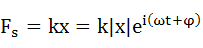・・・(6-6)

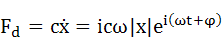・・・(6-7)

したがって、支持点の反力Ftは式(6-8)のようになります。

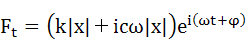・・・(6-8)

支持点の反力は複素数で表されるため、その大きさ|Ft|は式(6-9)のようになります。

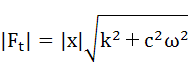・・・(6-9)

振動伝達率の定義は先にも述べましたが、支持点の反力|Ft|と入力される力Fの比(|Ft|/F)です。ここでは振動伝達率を表す記号としてλを用いることとします。

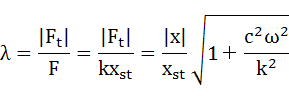・・・(6-10)

λ：振動伝達率

ここでFは入力荷重ですが、荷重を静的に加えた時の変位xstを用いてkxstと表されることに注意してください。さらに|x|に式(6-2)を代入して整理すると、式(6-11)のようになります。これが求める振動伝達率です。

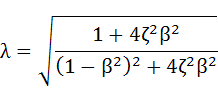・・・(6-11)

ここで、　、　　、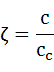　　

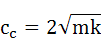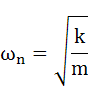
λ：振動伝達率、ζ：減衰比、c：減衰係数、cc：臨海減衰係数
、m：質量、k：ばね定数、ωn：固有角振動数

式(6-11)をグラフ化したものが図6-1です。

**図6-1　振動伝達率λとβの関係**

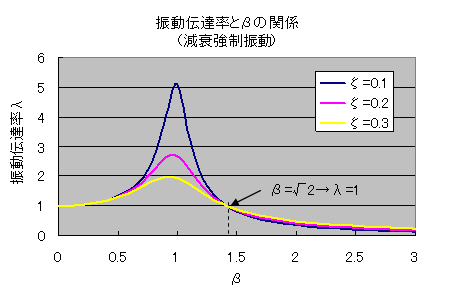このグラフから読み取れることは以下です。

振動を効果的に絶縁するためにはβは3以上が望ましいと一般的に言われています。βは大きければ大きいほどよいのですが、支持剛性がどんどん落ちてしまいますので、剛性の側面から現実的ではありません。実際にはある程度のところで妥協することになります。その辺が難しいところなのですが・・。

次項では今回の内容も踏まえて、"振動特性を考慮した構造設計の考え方"についてまとめてみたいと思います。