CAE技術者のスキルアップを応援します。 |
 |
5.減衰強制振動｜機械力学
計算モデル
1自由度の減衰強制振動のモデルを図5-1に示します。4の減衰自由振動に対して強制振動外力が追加されています。
 |
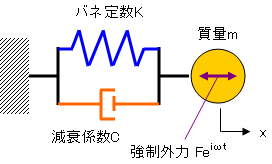この振動モデルを表す微分方程式は以下の式(5-1)のようになります。
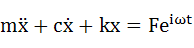・・・(5-1)
右辺は、Fの振幅、ωの角振動数で振動する強制外力を表していますが、sinとかcosを用いず、オイラーの公式を用いて複素数表記をしています。非減衰強制振動の時と同様に、今回も”虚部は無視し、実部のみが物理的な現象を表していると考える”という方針で立式しています。
解法
それでは解いていきます。また例によって式(5-1)の解を予め想定します。この場合、強制外力と同じ振動数で応答することが予測されますので、解の形も強制外力と同一で式(5-2)のようになります。
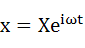・・・(5-2)
式(5-2)を微分していきます。1回微分が式(5-3)、2回微分が式(5-4)です。
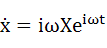・・・(5-3)
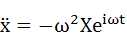・・・(5-4)
式(5-3)、式(5-4)を式(5-1)に代入します。
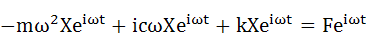・・・(5-5)
整理してXについて解いていきます。
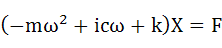・・・(5-6)
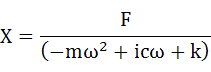・・・(5-7)
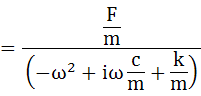・・・(5-8)
ここで式を解りやすくすることと、その特性を理解しやすくするために、各項を物理的意味において重要なパラメータに置き換えます。
まずは、k/mをωnを用いて式(5-9)のように置き換えます。ωnは非減衰自由振動モデルの固有角振動数を表します。
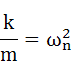・・・(5-9)
現在の減衰係数cと臨界減衰係数ccとの比を式(5-10)のように置き換えます。これも重要な意味を持ち、現在の減衰係数が臨界減衰係数に対してどのくらいかを表すパラメータになります。臨海減衰係数ccは式(5-11)です。
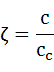・・・(5-10)
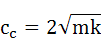・・・(5-11)
これらの置き換えを行って式(5-8)を簡略化していきます。
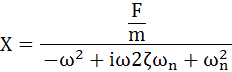・・・(5-12)
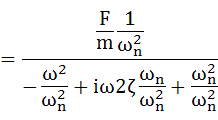・・・(5-13)
さらに式(5-14)のように、ω/ωnをβに置き換えます。これは強制外力の角振動数とこの系の固有角振動数との比になります。強制外力の角振動数と、この系の固有角振動数との関係が解り易くなるようβを導入します。ちなみにβ=1でそれらの角振動数が同一となり共振現象が発生することになります。
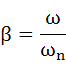・・・(5-14)
式(5-14)を式(5-13)に代入、及び式(5-9)を用いて、
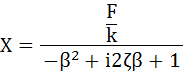・・・(5-15)
ここで、静的荷重に対する変位をXstで置き換えます。
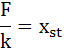・・・(5-16)
式(5-16)を式(5-15)に代入します。
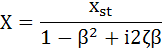・・・(5-17)
ここで、ちょっとした式変形をします。式(5-17)では分母に複素数が入ってしまっていますが、これを複数の表記としてa+ibのように変形させます。理由はこの方が後の計算で便利だからです。 やり方は簡単で分母および分子に分母の共役な複素数を乗じます。
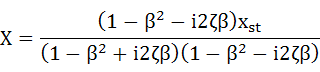・・・(5-18)
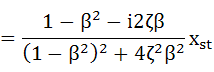・・・(5-19)
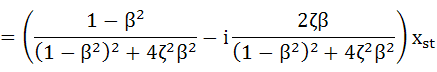・・・(5-20)
やや複雑ですが、a+ibの形式になりました。
ここで、図5-2の関係式を用います。この関係式は複素数a+ibをオイラーの公式を用いて、複素指数関数Re^(iθ)の形式に変換するものです。この公式を用いて式(5-20)の複素数の部分を変換します。
 |
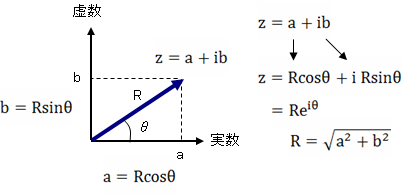図5-2の公式をそのまま適用したのが、下式(5-21)です。φは最後に書いていますが、式(5-25)のようになります。
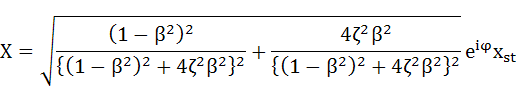・・・(5-21)
これを整理すると式(5-22)のようになります。かなりすっきりした形式にすることができました。
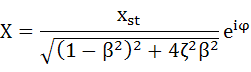・・・(5-22)
この式(5-22)を式(5-2)に代入します。
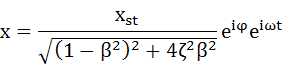・・・(5-23)
整理すると最終的に以下のようになりました。再度書きますが、”虚部は無視し、実部のみが物理的な現象を表していると考える”ということに注意してください。
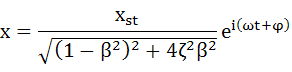・・・(5-24)
ここでφは式(4-25)のようになります。
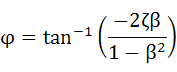・・・(5-25)
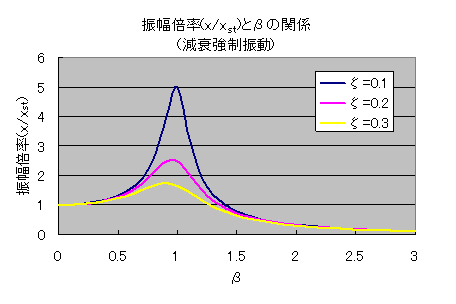
式（5-24）の振幅を表す部分Xを静的変位Xstで割った値である振幅倍率とβの関係を図5-3に示します。図5-4には式（5-25)で表される位相とβの関係を示します。
 |
 |
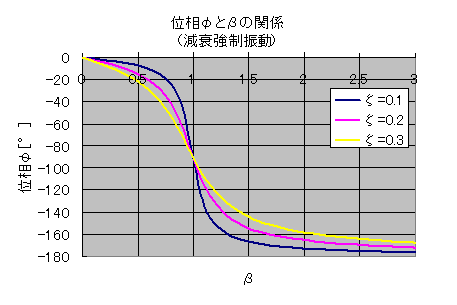図5-3より、減衰が大きくなるにつれてβ=1の時(共振時)の振幅が徐々に小さくなっていくことが確認できます。つまり、減衰は共振時の振幅を抑える働きがあるということです。位相については非減衰強制振動の時と同様にβ=1を境に逆転する傾向にありますが、減衰があることにより、徐々に位相が変化するような曲線になります。
実際の構造物には必ず何らかの減衰効果を含みますので、振動対策を考える上で今回の減衰強制振動は非常に重要です。次項では振動現象を考察する上では欠かせない振動伝達率について解説します。