TOP->CAE技術->機械工学->機械力学

3.非減衰強制振動｜機械力学

計算モデル

1自由度の非減衰強制振動のモデル図を図3-1に示します。2項の自由振動に対して強制外力が追加されています。このモデルでは強制外力が定義されますので、初期条件で同定するようなパラメータはなく、一意的にすべて決まります。


図3-1　1自由度非減衰強制振動

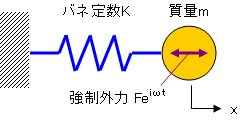この振動モデルを表す微分方程式を見ていきましょう。

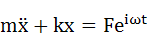・・・(3-1)

右辺は、Fの振幅、ωの角振動数で振動する強制外力を表していますが、sinとかcosを用いないでオイラーの公式を用いて複素数表記をしています。1項でも述べましたが、ここでもう一度オイラーの公式を用いる場合の方針をおさらいしましょう。

振動現象にオイラーの公式(複素数)を用いる場合の方針

  1. 共役な複素数の和とすることで、複素数を消去して実数の形式にする。
    または、
  2. 虚部は無視し、実部のみが物理的な現象を表していると考える。

今回は2の”虚部は無視し、実部のみが物理的な現象を表していると考える”という方針で解いていこうと思います。 ちなみに1の方法で強制外力項を表現するなら、F(e^(iωt)+e^(-iωt))/2というややこしい式になります。

解法

さて、例によって式(3-1)の解を予め想定します。この場合、強制外力と同じ振動数で応答することが予測されますので、解の形も強制外力と同一で式(3-2)のようになります。

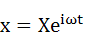・・・(3-2)

Xは振幅になりますが、これについてはまだ未知ですのでこれから同定していきます。この式についても虚部は無視して実部のみが物理的な現象を表していると考えます。

念のため、式(3-1)、式(3-2)で用いているオイラーの公式を以下に示します。

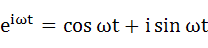・・・(3-3)

式(3-2)を微分していきます。1回微分が式(3-4)、2回微分が式(3-5)です。

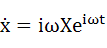・・・(3-4)

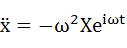・・・(3-5)

式(3-2)と式(3-5)を式(3-1)に代入します。

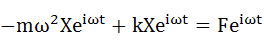・・・(3-6)

整理してXについて解きます。

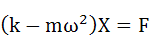・・・(3-7)

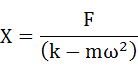・・・(3-8)

これで未知のパラメータXが求められましたので、式(3-2)に求めた式(3-8)を代入すれば終わりですが、各パラメータが今回の振動現象にどのように影響しているかを調べるために、さらに解り易い形に変形していきます。

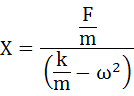・・・(3-9)

ここで、k/mをωnを用いて式(3-10)のように置き換えます。ωnは非減衰自由振動モデルの固有角振動数を表します。

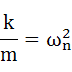・・・(3-10)

式(3-10)を式(3-9)に代入し、さらに変形していきます。

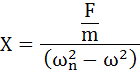・・・(3-11)

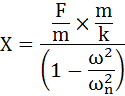・・・(3-12)

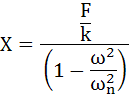・・・(3-13)

ここでF/kを式(3-14)のように置き換えます。これは静的にFの荷重を加えた時の変位を表しています。

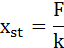・・・(3-14)

さらに式(3-15)のように、ω/ωｎをβに置き換えます。これは強制外力の角振動数とこの系の固有角振動数との比になります。強制外力の角振動数と、この系の固有角振動数との関係が解り易くなるようβを導入します。ちなみにβ=1でそれらの角振動数が同一となり共振現象が発生することになります。

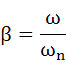・・・(3-15)

式(3-14)と式(3-15)を式(3-13)に代入します。

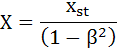・・・(3-16)

したがって、最終的には以下のようになります式(3-17)。これが式(3-1)の解です。ここで、その実部のみが今回の強制振動の現象を表していることに注意しなければなりません。

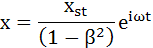・・・(3-17)

ここで式(3-16)の振幅を表す部分である式(3-16)がどのような特性を示すのか計算してみます。

図3-2に振幅倍率とβの関係をグラフにしたものを示します。
ここで、振幅倍率とは振幅xを静的荷重に対する変位xstで除した値です。


図3-2　振幅倍率とβの関係

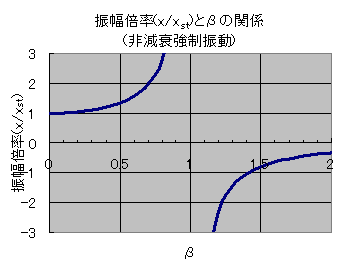この図から以下のようなことが読み取れます。

  • 0<β<1の範囲で振幅は1以下にはなり得ず、β=1に向かって急激にに増大する
  • β=1で共振状態になり振幅は無限大になる
  • β=1を境に位相が反転する(振幅の正負が反転)

今回は減衰がない状態を想定しましたが、実際の構造では必ず減衰があるため、共振したからと言って振幅が無限大になることはありません。次項からは減衰が振動現象にどのように影響しているのかを見ていきましょう。

[前へ]　|　[次へ]