2.非減衰自由振動|機械力学
計算モデル
本項では、最も簡単な振動モデルである1自由度の非減衰自由振動について解いていきたいと思います。解く方法としてはいろいろな方法がありますが、ここではオイラーの公式を用いて解く方法を説明します。
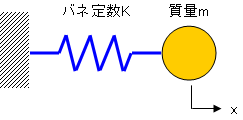
図2-1に1自由度の非減衰自由振動モデルのイメージを示しています。質量mの錘とバネ定数Kのバネを組み合わせ、バネの一方を剛壁に固定しただけの簡単なモデルです。
 |
この振動モデルを表す微分方程式は以下のようになります。
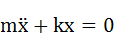 ・・・(2-1)
・・・(2-1)
xの上に2つのドッドが付いていますが、これは変位xを時間で2回微分することを表します。ドッドが1つなら1回微分です。
式(2-1)の第1項はxが2回微分されていますので加速度を表し、質量と加速度を乗じていますので、慣性力を表現しています。第2項はバネ定数と変位を乗じていますので、バネによる発生する力を表現していることになります。よって、式(2-1)全体で慣性力とバネ力釣り合っているということを言っています。これが減衰のない状態において振動現象を支配する法則です。
解法
この式(2-1)を解いていくわけですが、ここである仮定を導入します。これは明らかに振動する現象ですので、振動を表す関数、式(2-2)を解として仮定します。
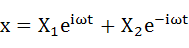 ・・・(2-2)
・・・(2-2)
ここで、Xは振幅、ωは角振動数、iは虚数単位、tは時間です。
e^(iωt)やe^(-iωt)の部分はオイラーの公式として非常に有名な式で、下式のようになります。
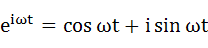 ・・・(2-3)
・・・(2-3)
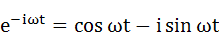 ・・・(2-4)
・・・(2-4)
式(2-2)は複素数を含んでいますが、e^(iωt)とその共役な複素数e^(-iωt)の和の形式にすることで複素数を消去し、全体として実数になるようにしています。
ここで、このように解を仮定する必然性は何かと疑問に思うと思います。オイラーの公式を利用する理由は、単に計算を簡単にするためです。この程度の計算であれば直接sinやcosを使っても解けますが、より複雑な問題になるとオイラーの公式を用いて計算した方が簡単になります。ただし、複素数を用いるのでその物理的意味を見失いがちですが、次の考え方を理解していれば、複素数の計算も受け入れられると思います。
振動現象にオイラーの公式(複素数)を用いる場合の方針
- 共役な複素数の和とすることで、複素数を消去して実数の形式にする。
または、 - 虚部は無視し、実部のみが物理的な現象を表していると考える。
今回は1.の”共役な複素数の和とすることで、複素数を消去して実数の形式にする”というやり方を採用しています。X1とX2が異なる値であると複素項が消去できないと思われるかもしれませんが、X1とX2を互いに共役な複素数とすることでうまく複素数を消すことができます。
2.の方法である”虚部は無視し、実部のみが物理的な現象を表していると考える”というやり方は、強制振動を解く場合に利用しますので、その項で説明します。
未知数がX1とX2の二つある理由としては、以下が挙げられます。
二つの未定係数X1とX2が必要な理由
- 2階の微分方程式を解くためには2度積分する必要があり、その都度2つの不確定な定数が現れる。そのため微分方程式の解には2つの未定係数を予め入れておく必要がある。
この未定係数を同定するためには、方程式とは別に2つの条件が必要で、今回の振動解析の場合、変位と速度の初期条件を用います。
仮の解として導入した式(2-2)はまだ解らないパラメータ(Xやω)を含む不完全なものです。それらのパラメータをこれから同定していきます。
まず、式(2-2)を微分していきます。
xを時間で1回微分。これは速度を表します。
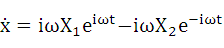 ・・・(2-5)
・・・(2-5)
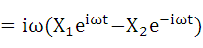 ・・・(2-6)
・・・(2-6)
xを時間で2回微分。これは加速度を表します。
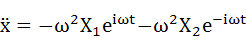 ・・・(2-7)
・・・(2-7)
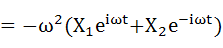 ・・・(2-8)
・・・(2-8)
式(2-7)と式(2-2)を式(2-1)に代入します。
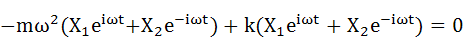 ・・・(2-9)
・・・(2-9)
式(2-9)を整理してωについて解いていきます。
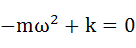 ・・・(2-10)
・・・(2-10)
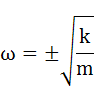 ・・・(2-11)
・・・(2-11)
式(2-11)はこの振動系の固有角振動数を表しています。物理的には正の値のみ意味を持ちます。ここで、式を簡単にするため、式(2-11)のルートの部分を下式のように置きます。
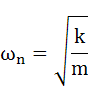 ・・・(2-12)
・・・(2-12)
この固有角振動数ωnを2πで割ると固有振動数(固有周波数)になります。今は非減衰自由振動について計算していますが、もしこの振動系に固有振動数と同じ振動数で外力が入力されたなら、共振現象が発生することになります。我々技術者は、このような共振現象が発生しないように事前にその振動数を予測して、予め手を打っておくことが重要になります。
ここで重要なのは、固有振動数はバネ定数のルートに比例し、質量のルートに反比例するということです。共振問題で対策を検討する場合、その問題としている振動系の固有振動数を変化させることをよくやりますが、その場合、剛性(K)を2倍にしてもその固有周波数は√2倍にしかなりません。また質量についても同様に、その変化分のルートしか効きません。このような関係は技術者の基礎知識として理解しておく必要があります。
さらに計算を進めます。
式(2-12)を式(2-2)に代入します。
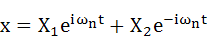 ・・・(2-13)
・・・(2-13)
更に、式(2-3)、式(2-4)を式(2-13)に代入します。
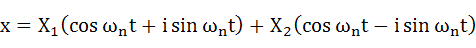 ・・・(2-14)
・・・(2-14)
式(2-14)をcosとsinについて整理します。
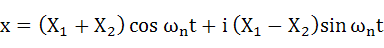 ・・・(2-15)
・・・(2-15)
初期速度に対する条件を導入するために、式(2-15)を微分します。
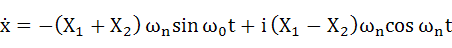 ・・・(2-16)
・・・(2-16)
ここで式(2-15)と式(2-16)に初期条件を設定して未知数を求めていきます。
初期条件とはt=0の時の状態です。
 ・・・(2-17)
・・・(2-17)
式(2-17)を式(2-15)に代入して下式を得ます。これをt=0の時の変位ということでX0とします。
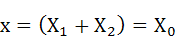 ・・・(2-18)
・・・(2-18)
式(2-17)を式(2-16)に代入して下式を得ます。これをt=0の時の速度ということでV0とします。
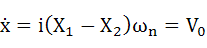 ・・・(2-19)
・・・(2-19)
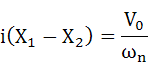 ・・・(2-20)
・・・(2-20)
上式は複素数iが入っていますが、全体として実数です。式(2-18)と式(2-19)をX1、X2について解くと解りますが、X1とX2は互いに共役な複素数の値になるのです。したがって、X1+X2は実数の項のみ残るのでそのままでよいのですが、X1-X2は複素数の項のみ残るため、それにiを乗じたものは全体として実数の形式になっています。
式(2-18)と式(2-20)を式(2-15)に代入します。
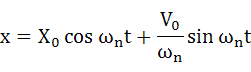 ・・・(2-21)
・・・(2-21)
式(2-21)でも答えになりますが、一般的には以下の式まで計算して位相との関係が解るようにします。
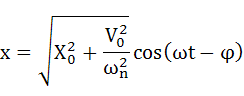 ・・・(2-22)
・・・(2-22)
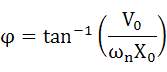 ・・・(2-23)
・・・(2-23)
ここで、以下の公式を利用してます。この式(2-24)、式(2-25)の公式も重要ですので覚えておくと便利です。
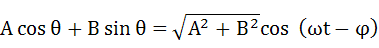 ・・・(2-24)
・・・(2-24)
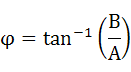 ・・・(2-25)
・・・(2-25)
式(2-22)が1自由度の非減衰自由振動の解になります。今回はオイラーの公式を用いて解く方法を説明しましたが、いろいろな方法で解くことができます。ぜひご自分でチャレンジしてみてください。
