TOP->CAE技術->FEMを体感しよう

4.境界条件の設定｜FEMを体感しよう

解析条件

はじめに前項で求めた解析モデル全体の連立方程式を改めて以下に示します。この式(3-5)に要素の特性を具体値として入力し、更に今回のテーマである境界条件を設定して解ける形にしていきましょう。

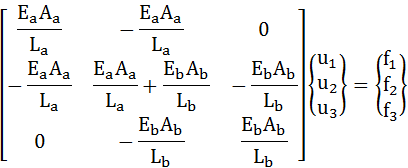・・・(3-5)

ここで今回の解析モデルに具体的な値を入力していきます。どのような条件でもよいのですが、今回は図4-1に示す解析条件で解くことにします。

**図4-1 解析条件**

要素aとbでは異なる断面積、長さを設定しています。弾性率は同じとしました。まずはこの要素特性を代入していきましょう。

要素剛性マトリクスの成分はプラスかマイナスかの違いはありますがすべてEA/Lです。それぞれの要素でEA/Lを計算してみますと、要素aで105000、要素bで70000になります。節点2は共有節点ですのでそれぞれの成分を足し合わせて105000+70000=175000になります。これらを式(3-5)に代入したものが下式(4-1)です。

・・・(4-1)

これはメッシュだけ切った状態の解析モデルに材料特性や板厚、あるいは断面特性などを設定していく作業に近いですね。

境界条件(荷重、拘束条件)の設定

次に荷重条件を設定します。図4-1の条件では節点3に対して10000Nの荷重を与えていますので、これに対応する荷重ベクトル｛f｝の成分f₃に10000と入力します。その他の成分はとりあえず0と入力しておきます。

・・・(4-2)

次に拘束条件を設定します。図4-1の条件では節点1を固定しています。固定とはどういうことかというと変位を0にするということです。したがって変位ベクトル｛u｝の成分u₁に0を入力します。

・・・(4-2)

ここでu₁に0を入力したということは、その項が既知になったということですので、全体剛性マトリクスの1行目が不要になります。また、既知になったu₁=0を全体剛性マトリクスに展開すると、一列目がすべて0になります。その手順を示したのが図4-2になります。

**図4-2 拘束条件設定による剛性マトリクスの自由度減少**

ということで最終的に解くべき連立方程式は下式(4-3)になります。

・・・(4-3)

上式(4-3)では自由度が1減って2自由度になっています。このように拘束条件を設定すると、設定した数だけ自由度が減ることになります。極端なことを言えば、すべての節点を拘束した場合は解くべき自由度は0となり、計算する必要がなくなります。これは求める変位ベクトル｛u｝に、拘束条件を設定することにより0または強制変位値が入力され、すべての値が既知になるためです。そんなことはしないと思いますが・・・。

ここで重要なことは以下です

拘束条件(強制変位も同じ)を設定することは、変位ベクトル｛u｝に値を入力することと同じである。
荷重条件を設定することは、荷重ベクトル｛f｝に値を入力することである。
拘束条件を設定した数だけ、解くべき自由度が減る。

有限要素法構造解析では変位ベクトル｛u｝を解くことが目的です。ひずみや応力などは変位が求められた後に2次的に計算される値となります。　

本項により、境界条件が連立方程式上でどのように処理されるか理解できたでしょうか？FEM解析ソフトウェアはこの辺の理論的なことをブラックボックス化して簡単に使うこともできますが、このような内部的な処理を頭の中でイメージできることは、解析業務を遂行する上で非常に重要なことだと考えます。少々複雑に見えますが、やっていることは機械的な処理ですので落ち着いて考えれば理解できると思います。

　これで解析を実行する準備が整いました。次項では実際に式(4-3)を解き、考察してみたいと思います。

[前へ]　|　[次へ]

FEMを体感しよう