07-2.ランダム応答解析|動解析入門
振動を統計的に取り扱うための準備
ランダム応答解析では振動の時系列波形を議論するのではなく、パワースペクトル密度関数(PSD)や標準偏差などのパラメータを用いて振動を取り扱います。これらを理解するために必要な定義を説明していきます。
平均値
ランダム波形の関数をx(t)とすると、x(t)の平均値は下式となります。積分の形式となっていますが、意味するところは単純な時間平均です。
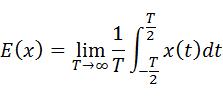 ・・・(7-2-1)
・・・(7-2-1)
ちなみにランダム応答解析ではE(x)=0の振動波形が想定されます。
自乗平均値
x(t)の自乗平均値は下式となります。
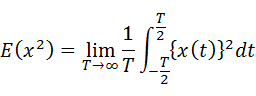 ・・・(7-2-2)
・・・(7-2-2)
理論的には3乗平均、4乗平均・・・など高次に展開できますが、通常は自乗(2乗)平均までを取り扱います。
分散
平均値まわりの自乗平均値は分散と呼ばれ、下式となります。
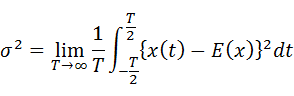 ・・・(7-2-3)
・・・(7-2-3)
平均値E(x)=0の場合、分散と自乗平均値は等しくなります。
標準偏差
分散の平方根は標準偏差となります。標準偏差はσで表記します(応力の意味のσではないことに注意)。
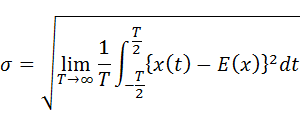 ・・・(7-2-4)
・・・(7-2-4)
分散とか標準偏差という用語が出てくると、何となく統計的な感じがしてきますね。
実効値(RMS値)
平均値E(x)=0の場合の標準偏差は自乗平均の平方根となり、いわゆる実効値(RMS値)と等しくなります。
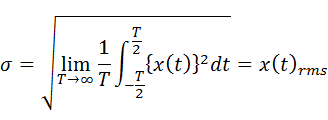 ・・・(7-2-5)
・・・(7-2-5)
ランダム応答解析では平均値E(x)=0の振動を取り扱いますので、標準偏差=実効値となります。
自己相関関数
自己相関関数はx(t)の時刻をτだけオフセットさせたx(t+τ)とx(t)とを乗じた値の平均として下式のように定義されます。
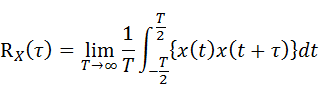 ・・・(7-2-6)
・・・(7-2-6)
自己相関関数は時系列データの周期性を評価するのに使用されます。自己相関関数はτが0の時に最大値をとる性質があります。データの不規則性が強い場合、τ=0以外での値は小さくなります。周期性がある場合、あるτの値でピークが表れ、その間隔で周期が解ります。
自己相関関数はτ=0で下式のようになり、自乗平均を求める式と等しくなります。
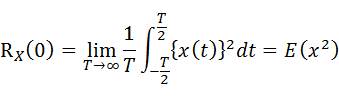 ・・・(7-2-7)
・・・(7-2-7)
パワースペクトル密度関数(PSD)
パワースペクトル密度関数(PSD=Power Spectral Density)は自己相関関数をフーリエ変換したものとして定義されています。
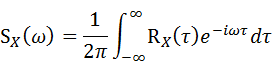 ・・・(7-2-8)
・・・(7-2-8)
PSDは1Hz幅当たりのパワー値を表します。
パワースペクトル密度関数と標準偏差
パワースペクトル密度関数の逆変換は、
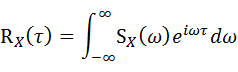 ・・・(7-2-9)
・・・(7-2-9)
τ=0とすれば、
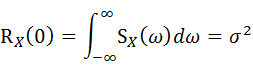 ・・・(7-2-10)
・・・(7-2-10)
上式の右辺はPSD曲線とω軸とで囲まれる面積を表します。また左辺はτ=0とおいたときの自己相関関数となりますが、これは自乗平均値と等しくなります。ランダム応答解析では平均値=0の振動を取り扱いますので、自乗平均値=分散となります。また、分散の平方根は標準偏差となります。
いろいろ難しくなってきましたが、PSD曲線とx軸とで囲まれる面積の平方根は標準偏差を表すということだけ理解してください。
応力PSDの場合には下図のようになります。
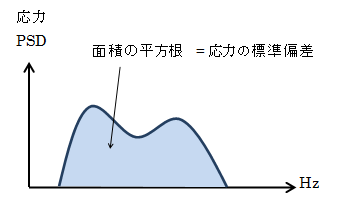
ランダム応答解析で強度を評価する際には実際の応力値ではなく、応力の標準偏差を用いて統計的に評価することになります。解析ソフトウェアによっては標準偏差とは呼ばない場合も多く、自乗平均平方根や実効値(RMS値)、Abaqusでは平方自乗平均など、いろいろな言い方があるので混乱することがあります。しかしどれも同じことを言っています。ここでは統計的な意味合いを強調するために、標準偏差と呼ぶことにします。
正規分布の確率密度関数
統計に関しての詳細は専門の書籍やその他のホームページを参考にしていただくとして、ここでは正規分布の確率密度関数と標準偏差の関係だけ説明します。
データのバラツキが正規分布(=ガウス分布)に従うとすれば、その確率密度関数f(x)は下式のように表されます。
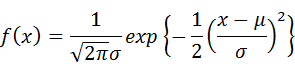 ・・・(7-2-11)
・・・(7-2-11)
f(x):確率密度関数、σ:標準偏差、μ:平均値
特に平均値μ=0、分散σ^2=1の分布は標準正規分布と呼ばれます。
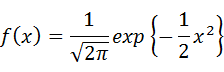 ・・・(7-2-12)
・・・(7-2-12)
正規分布をグラフで表すと下図のようになります。
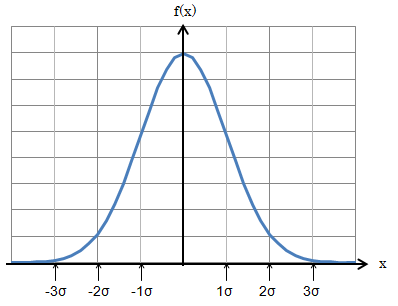
この確率密度関数f(x)を任意の区間で積分することで、その範囲にxが入る確率P(x)を求めることができます。
例えば、a〜bの範囲にxが入る確率は下式のようになります。
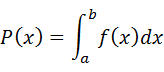 ・・・(7-2-13)
・・・(7-2-13)
ただしこの積分が厄介で公式などを使って直接積分できないため、通常は数値積分を使って計算します。標準偏差σ整数倍の範囲で積分すると下記のようになります。
- ±1σの範囲で積分:P(x)=0.6826
- ±2σの範囲で積分:P(x)=0.9544
- ±3σの範囲で積分:P(x)=0.9974
ということはつまり、
- ±1σの範囲に入る割合:68.26[%]
- ±2σの範囲に入る割合:95.44[%]
- ±3σの範囲に入る割合:99.74[%]
ということです。
単位時間当たりに閾値αを超える回数
強度的な評価で重要な閾値(強度的な許容値など)通過の頻度は下式により求めることができます。
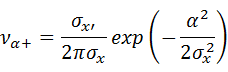 ・・・(7-2-14)
・・・(7-2-14)
να+:単位時間当たりにαを超える回数、σx’:速度の標準偏差、
σx:変位の標準偏差、α:閾値
等価振動数(または等価期待振動数)
上式のαを0とすると、0を単位時間当たりに通過する回数となります。これは等価振動数または等価期待振動数と呼ばれます。
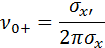 ・・・(7-2-15)
・・・(7-2-15)
ν0+:単位時間当たりに0を通過する回数(等価振動数)、
σx’:速度の標準偏差、σx:変位の標準偏差
強度を評価するためには、どのくらいの頻度で振動するかが重要です。しかし通常私たちが扱う多自由度系の構造の場合には、複数の固有モードが存在するために、単一の振動数で表すことができません。そこで統計的に妥当な等価振動数という概念が必要になります。
今回は変位、速度を用いましたが評価対象が応力ならば、それぞれ応力、応力速度を用います。対象が1自由度の振動の場合、等価振動数は系の固有振動数に一致します。しかし多自由度系の場合、必ずしも固有振動数に一致せず、しかも同じ構造内で評価点や評価する値によって異なることもあります。
荷重定義
ランダム応答解析における入力荷重はいろいろな定義方法がありますが、一般的に強制運動加振として加速度のPSDを定義することが多いです。PSDは振動試験の規格で決まっているものを参照したり、実機の稼働状態における振動加速度を測定し、信号処理によってPSDに変換したものを利用したりします。
