TOP->CAE技術->動解析入門

04.周波数応答解析｜動解析入門

周波数応答解析とは？

周波数応答解析は単純な正弦波の入力に対する定常的な応答を求める解析手法です。通常は一つの周波数だけでなく、ある周波数範囲に対し、ある周波数刻みで解析し、全体的な応答の特性を把握するのに用いられます。入力を与える手段としては、一般的な荷重の他、強制運動(変位、速度、加速度)で与えることができます(強制運動に対応していないソルバーもあります)。応答としては各節点における変位、速度、加速度、またそれにより生じる要素の応力などを評価することができます。

一般に周波数応答解析の手法としてはモード法と直接法があります。それぞれの特徴は以下の通り。

直接法

計算負荷が高い
モードの打ち切り誤差がないため精度が高い
モード減衰が利用できない(全体減衰、材料減衰、減衰要素、等を利用する)

モード法

計算負荷が軽い
モードの打ち切り誤差が発生する
モード減衰が利用できる

(参考)
モード法の周波数応答、過渡応答解析におけるモード数 (モードの打ち切り誤差について説明)

両手法で計算負荷や精度の違いはありますが、モデル化上の違いとしては減衰の取り扱いです。構造物に発生する減衰の原因となるものは非常に複雑なメカニズムが絡むため、材料減衰や減衰要素等だけでは正確に再現させることが困難です。

その点、モード法ではモード減衰が利用できるため、モードごとに異なる減衰特性を定義することができます。モード減衰は複雑なメカニズムで発生する減衰をすべて1つに丸め込んだ減衰ですので、実験でモード減衰を同定して解析モデルに入力することで、構造の減衰特性を再現させることができます。

周波数応答解析の用途

繰り返しになりますが、周波数応答解析は単純な正弦波の入力に対する構造の定常的な応答を求める解析手法です。入力荷重を1Nなど単位荷重とすれば、入力から応答点までの伝達関数を簡易的に求めることもできます。つまり構造の周波数応答特性(どの周波数でどのくらいの応答を示すのか)を把握するのに用いられます。また、構造の実稼働状態での入力荷重が正弦波であるならば、その時発生する振動レベルや各部の応力なども評価することができます。

解析例

Abaqusチュートリアルの『周波数応答解析(モード法)』の項で解析した事例を紹介します。

解析対象は単純なプレートの片方を固定した片持ち梁です。

プレート寸法：300×50×1.2
材料：鉄鋼材料を想定(E=210GPa,ρ=7.85e-6kg/mm^3,ν=0.3)
境界条件：片側の端部を完全固定
固有値抽出範囲：1～500Hz
梁の先端に1Nの正弦波荷重(周波数範囲：1～100Hz)
減衰：1～500Hzの範囲で減衰比0.05

この条件で周波数応答解析を実施した結果は以下です。

加速度応答

下図ではプレート先端の加速度[mm/s^2]を示しています。

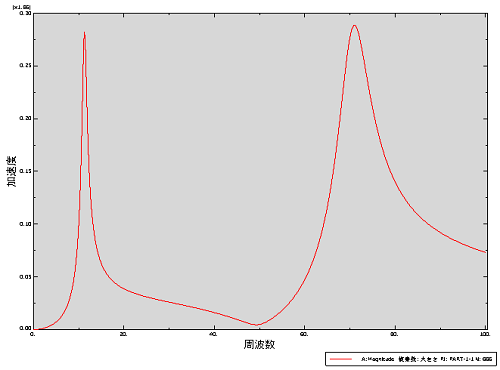
前項で示したように入力荷重の周波数範囲(1～100Hz)には11.3Hz(モード1)、70.6Hz(モード2)に固有モードが存在します。今回の周波数応答解析ではこの固有振動数付近で応答レベルが大きくなっています。これが共振現象です。固有モードが存在するので当然の結果ですが、周波数応答解析ではこの共振時の応答レベルがどの程度になるかを予測することができます(減衰値が正確に同定されていることが前提ですが・・)。上図の例では11.3Hz(モード1)付近で最大281000mm/s^2、70.6Hz(モード2)付近で288000mm/s^2程度です。

変位応答

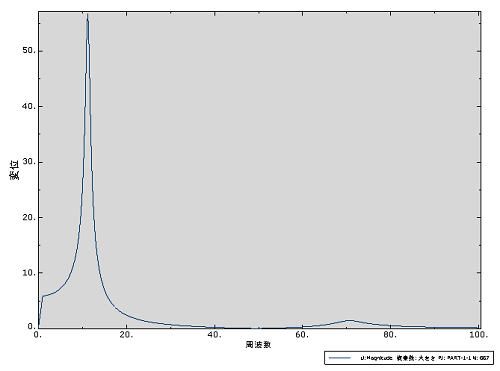
下図はプレート先端での変位を示したグラフです。11.3Hz(モード1)付近では56.8mmも変位しています。もはや線形解析の範疇を超えていますね・・。70.6Hz(モード2)付近では1.46mm程度です。

応力レベル

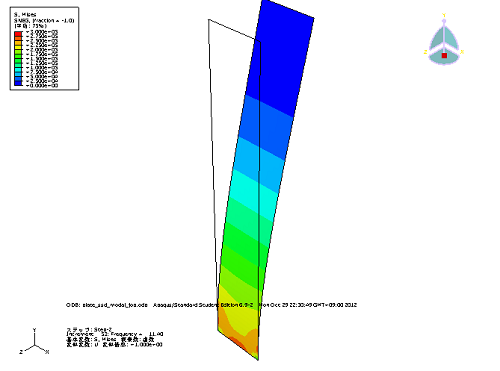
<11.3Hz(モード1)付近の応力分布図>

下図のような変形モードで拘束部付近に240N/mm^2程度の応力が発生しています。(変位スケール：1倍、応力レンジ：0～300N/mm^2)

<70.6Hz(モード1)付近の応力分布図>

下図のような変形モードで拘束部付近にで30N/mm^2程度の応力が発生しています。(変位スケール：20倍、応力レンジ：0～50N/mm^2)

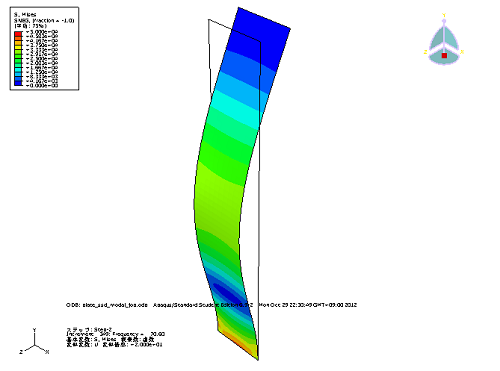
※：複素数の変形モードを大きさで表現すると変なことになるので、図では支配的だった虚数成分の変形を示しています。値を評価するときは大きさで見る必要があります。

<拘束部付近の応力>

下図は拘束部から少し離れた場所のミーゼス応力の応答です。

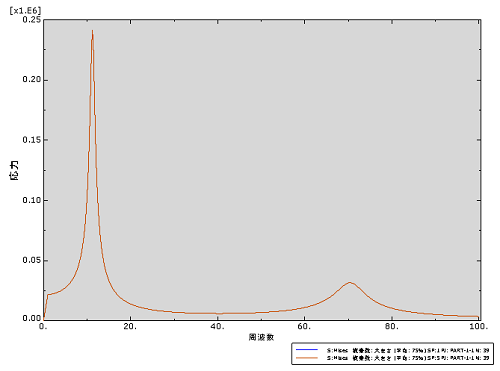
周波数応答解析の重要な特徴は入力が正弦波に限られるということです。そしてその正弦波の入力に対する定常的な応答が計算されます。しかし実際のモノの入力荷重は時間的にも周波数的にも複雑な波形となることも多いですので、これによる構造側の応答は周波数応答解析で求めることができません。実はこれを解析するのが次項で説明する過渡応答解析になります。

[前へ]　|　[次へ]