CAE技術者のスキルアップを応援します。 |
 |
3.全体剛性マトリクス｜FEMを体感しよう
解析モデルの定義
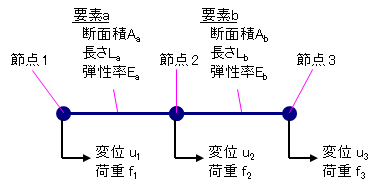
まずはじめに今回の1次元ロッド要素を用いた解析モデルの外観を図3-1に示します。単に2つのロッド要素がつながっただけですが、皆さんが普段メッシュを切っている作業も実は規模が異なるだけでこれと同じことなのです。この要素は1次元なので数を増やしても単に長くなっていくだけであまり実用的ではありませんが、2次元や3次元要素なら要素をつなぎ合わせて全体の形状を表現できるようになります。今回はあくまでサンプルで内部的な処理を理解していただくことが目的なのであしからず。
 |
全体剛性マトリクスを求める
ここで前項で求めた要素剛性マトリクスを改めて示します。
・・・(2-12)
図3-1の解析モデルでは要素を2つ使用して、それぞれ要素a、要素bとしています。また、断面積、長さ、弾性率などの各パラメータはそれぞれの要素で異なるとして、aまたはbの添え字をつけて区別することとします。
まずはじめにそれぞれの要素の要素剛性マトリクスを求めていきましょう。
要素aについて式(2-12)に当てはめると以下のようになります。
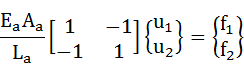・・・(3-1)
単にE、A、Lに要素を識別するための添え字aがついただけですね。ここで、次工程で計算しやすくするためにマトリクスの外に出ていたEA/Lの項をマトリクスの中に入れます。
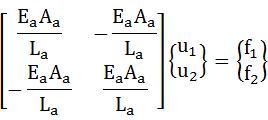・・・(3-2)
要素bについても同様に
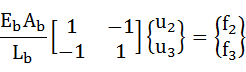・・・(3-3)
要素bは節点2と節点3を使用しているので{u}と{f}の項の添え字に注意してください。ちなみに節点2は要素1と共有しているので、そこに発生する変位や力は要素1と要素2で同値となります(厳密に言うとf2は要素a側の力と要素b側の力を足したものになります)。したがって、要素2の式でも同じ記号(u2、f2)を使用しています。
式(3-3)についても同様にEA/Lの項を括弧の中に入れておきます。
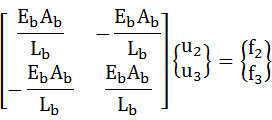・・・(3-4)
式(3-2)と式(3-4)を重ね合わせて全体剛性マトリクスを構成する方法を下図で説明します。
 |
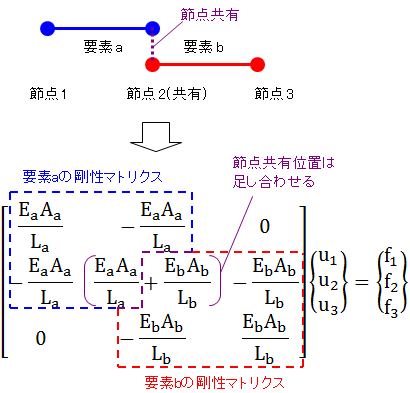図3-2で上側に書いている図が要素を節点2で結合させる場合のイメージを示しています。これを数式に対応させたのがその下の式になります。 ポイントは要素が共有している節点に対応するマトリクス成分を足し合わせるということです。変位ベクトルや荷重ベクトルはその対応関係を保つように番号順に並べます。
このようにして組み立てた[K]マトリクスを全体剛性マトリクスと呼びます。図3-2にも示していますが、改めて下式に示します。この式(3-5)が解析モデル全体を表す連立方程式になります。
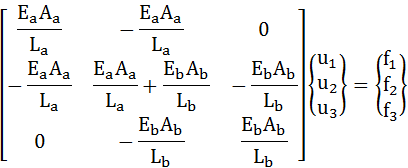・・・(3-5)
この手順は要素が増えても、あるいは2次元、3次元などの実用的な要素になっても同じです。今回は3×3のマトリクスになりましたが、皆さんが実務で行っている解析モデルでは、このマトリクスサイズが数十万とか数百万とか、非常に大きなサイズになると思います。
このマトリクスサイズは何によって決まるかというと、自由度の数です。例えば今回の場合、一つの節点に許される変位はx方向のみになるので、節点当たり1自由度です。2つの要素をつなげた場合、モデル全体として3つの節点があるので、自由度数は3になります。つまり自由度数は節点当たりの自由度×節点数で計算できます。全体剛性マトリクスのサイズは自由度数×自由度数で表され、今回の場合は3×3になります。
ちなみに実用的な要素では一つの節点に複数の自由度を持っています。例えば、3次元要素の節点当たりの自由度はxyzの3方向で3自由度、シェル要素で5自由度や6自由度、1次元要素のビーム要素などでは6自由度あります。よって解析モデル全体の自由度数や全体剛性マトリクスのサイズは、例え同じ節点数であったとしても使用する要素により異なるということも理解しておいてください。